Here you can find the slides of some recent talks of mine.
Resurgence and topological strings
|
In the StringMath 2023 conference at Melbourne I summarized recent results on the resurgent structure of topological string theory on Calabi-Yau manifolds. This is a beautiful and non-trivial example of Ecalle's ideas, and also a new road to understand BPS invariants in terms of Stokes constants. The slides of the talk can be found here (the picture on the left is courtesy of Johanna Knapp and was taken in an excursion during the conference). The video of a related talk can be found here.
|
Resurgence in low-dimensional quantum systems
|
At the workshop "Exact quantization and applications to condensed matter physics", held at SISSA in Trieste in September 2021, I gave three lectures on resurgence in low-dimensional quantum systems. After a general introduction to resurgence with illustrations in quantum mechanics, I describe in detail resurgent trans-series associated to renormalons in various low-dimensional quantum theories, like the Gaudin-Yang model, the Gross-Neveu model and other integrable models. The slides can be downloaded here.
|
Three lectures on resurgence and quantum topology
|
These are the slides for my three lectures at the Young Researchers Symposium in the ICMP 2021. After a general introduction to resurgence techniques and ideas, I give a pedagogical overview of my recent work with Stavros Garoufalidis, Jie Gu and Campbell Wheeler on the resurgent structure of quantum knot invariants. The first lecture can be found here, the second one here, and the third one here. A write-up of the lectures with some additional information can be found here. This is a closely related talk, intended for mathematicians.
|
Resurgence and quantum knot invariants
|
This talk is based on a 2020 paper written with Stavros Garoufalidis and Jie Gu. It gives a detailed description of the resurgent structure of the perturbative knot invariants obtained from state integrals, for hyperbolic knots. It also reports on work on progress on similar structures appearing in topological string theory. The slides can be downloaded here. A slightly different, less technical version can be found here.
|
An overview of resurgence
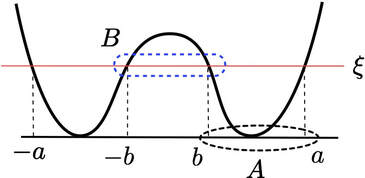
This talk gives an overview of resurgence and its bearing on non-perturbative effects in quantum theory. It discusses in particular the WKB method in quantum mechanics and the recent application to superconductivity explained in my joint 2019 paper with Tomás Reis. The slides can be downloaded here.
My take on quantum curves
|
Quantum curves have been recently at the center of the interaction between geometry and quantum field theory/string theory, and they have been studied from many different perspectives. In this talk, given in Banff in 2018, I try to explain my point of view on quantum curves. I emphasize the importance of having a Hilbert space in the construction, and argue that the Fredholm determinant of the quantum curve is the crucial ingredient linking geometry and spectral theory. The slides can be downloaded here.
|
Stringy geometry
"Stringy geometry" is one of the most important circle of ideas produced by string theory. In this SwissMAP colloquium, given in 2017, I give my viewpoint on the subject. I emphasize the importance of incorporating string interactions in the geometric picture, and I point out how this can be achieved by a fully quantum-mechanical dual to string theory, in the spirit of the AdS/CFT correspondence. The slides can be downloaded here.





