Here you can find some of my lecture notes, based on different courses I have given, mostly at the University of Geneva. The notes are in English, unless stated otherwise.
Les Houches lectures on non-perturbative topological strings
|
In August 2024, the summer school at Les Houches was devoted to quantum geometry, with a great panel of lecturers and topics. You can find the details and lectures notes for the school in this webpage. In the last week of the school I gave some pedagogical lectures on non-perturbative topological strings, where I first covered their resurgent structure and the connection to BPS invariants, an then introduced the TS/ST correspondence between Topological Strings and Spectral Theory, which provides a non-perturbative definition of the former on toric Calabi-Yau manifolds. A written version of the lecture notes can be found here. The lectures contain many exercises, and some of them involve writing Mathematica programs. Most of the solution programs can be found here. Feedback and improvements are welcome!
|
An introduction to resurgence in quantum theory
|
Most introductions to resurgence focus on formal and mathematical aspects. These lecture notes are based on a course devoted to applications of resurgence to quantum theory. The course has three parts. The first one is a summary of basic resurgent tools (Borel transform, Borel resummation, Stokes automorphism). The second part shows how this formalism gets incarnated in one-dimensional quantum mechanics. The third part explores what is known about resurgence in QFT, focusing on the renormalon problem. The notes can be donwloaded here, and two Mathematica programs with worked out examples can be found here.
|
An introduction to topological string theory
|
These lectures notes are based on a course I gave long ago in Hamburg. They present an introduction to topological string theory with emphasis on the special geometry of Calabi-Yau manifolds and the holomorphic anomaly equations of BCOV. I revisited them for a recent project and I tried to provide a detailed description of various aspects of the B-model, like e.g. the theory of propagators. The general theory is illustrated with the example of the quintic Calabi-Yau manifold. You can find the notes here.
|
Path integrals in quantum theory
This is a course at the doctorate level on path integrals in quantum theory. It starts with the standard path integral formulation of the quantum mechanics of a single particle, and moves on to derive the path integral formulation of quantum many-particle systems. The general formalism is illustrated with applications to interacting quantum gases. The lecture notes can be found here.
Statistical mechanics
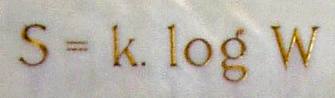
This is an advanced undergraduate level course on statistical mechanics. An interesting peculiarity of the course is that it contains an introduction to two of the most beautiful models in non-equilibrium statistical physics: the Kac ring model, and the Ehrenfest urn model. You can download the lecture notes (in French) here.
An introduction to topological quantum field theory
This is an introduction to topological quantum field theory at the master level. Shortly after the beginning of the course, COVID and confinement took over our lives and I never got as far as I was planning. The course contains however an introduction to supersymmetry and to the Mathai-Quillen formalism, and a discussion of the Witten index in supersymmetric quantum mechanics. You can download the lecture notes here.
Mathematical models for animals and humans
This course is an introduction to mathematical modelling based on game theory. It contains applications to economics and to animal behaviour. Although I never did research in this field, game theory has been a hobby of mine for some time now, and I was lucky enough to be able to transform this hobby into a fun course. You can download the lecture notes here.
Classical and quantum mechanics for mathematicians
Here is the challenge: you have thirty-two hours to teach both classical and quantum mechanics to mathematicians, at the master level. What do you do? This was, alas, no thought experiment, but a real one. The lecture notes resulting from the experiment can be found here. I hope they are useful.
An introduction to differentiable manifolds
This is an introduction to differentiable manifolds for advanced undergraduates in mathematics. The lecture notes (in French) can be downloaded here.
Quantum field theory in curved space
This is a course on quantum field theory in curved space at the master/doctorate level. I'm clearly not an expert on the topic, so the course is not very insightful, but it is detailed and might be useful. You can find the lecture notes here.
An introduction to non-perturbative effects in string theory and AdS/CFT
In 2015 I gave a series of lectures at ICTP in Trieste on non-perturbative effects in AdS/CFT and in string theory, where I start with a general introduction from the point of view of resurgence. The lecture notes can be found here.
Topological field theory and four-manifolds
These are the notes of a course I gave long ago in Villa de Leyva (Colombia). It is probably superseded by my joint book with José Labastida, but it might be still useful for learning the subject. You can find the lecture notes here.
General topology
This is an undergraduate course on hyperbolic geometry and general topology. The lecture notes (in French) can be found here.